Finite Length Dipole Antenna

Hello everyone, this time I am going to share with you a project I did for my antennas class. It consist of  calculating and plotting the parameters of a FINITE LENGTH DIPOLE antenna on paper and using Matlab.

Well, the first thing you have to do is to read Chapter 4 (Linear Wire Antennas) (4.5 Finite Lenght Dipole) of the book ANTENNA THEORY Analysis and Design, 3th edition, author: Constantine A. Balanis.

All the parameters that are treated in 4.5 of the book, are plotted and calculated with Matlab (.mfile uploaded) and calculated on paper (Pdf file uploaded).

How to use the Matlab file: 

1. Download the mfile.

2. Write on Matlab addpath (and the location where you downloaded the mfile)

       Example: addpath c:\matlab\work

3. Run the function on Matlab. But first you have to change L by the lenght of the dipole in wavelength, ra by the radius of the dipole in wavelength, frec by the frequency you design the dipole in hz. The function is the following:

[Rr,Xm,Rin,Xin,Prad,Emax,Wavmax,Umax,Do,DdB,Aem]=antenaFelixRuiz(L,ra,frec)

All the parameters for this antenna are calculated assuming that the diameter is considerably smaller than the operating wavelength. And these are only for a dipole of wavelength between 0 and 3 wavelengths, 0<= Lambda<=3. When you run the mfile and do the calculations you have to obtain the following parameters shown in the figure.

For example:

For a half-wavelength dipole of radius 5mm. and a frequency of 100Mhz, we have a radius of 0.0016 wavelength.

Call the function:

[Rr,Xm,Rin,Xin,Prad,Emax,Wavmax,Umax,Do,DdB,Aem]=antenaFelixRuiz(0.5,0.0016,100*10^6)

Rr =

   73.1296

Xm =

   42.5445

Rin =

   73.1296

Xin =

   42.5445

Prad =

   36.5648

Emax =

   40.0000

Wavmax =

    2.1221

Umax =

    4.7746

Do =

    1.6409

DdB =

    2.1509

Aem =

    1.1752

Figure n°1 Current distribution.

figure n°2 Electric field pattern (in linear scale)

figure n°3   3D Electric fiel pattern

figure n°4 Linear plot of Electric field pattern (lobes)

figure n°5 Poynting vector

figure n°6 Radiation intensity

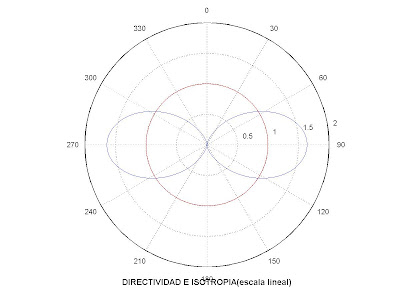
figure n°7 Directivity and isotropy (dimensionless)

figure n°8  3D Directivity and isotropy

Mfile (Matlab file) link1

Mfile (Matlab file) link2

Pdf calculations on paper link1

Pdf calculations on paper link2